この記事のポイント
投資に興味を持つ人が増えてきていますが、Excel(エクセル)には複利計算のできる関数が用意されているため、エクセルで積立額の算出が可能です。
今回はエクセルにある、複利の計算が可能なFV関数について解説します。
複利の利回り計算をしたい人は、ご自身でエクセルを使って楽しんでみてはいかがでしょうか?FV関数はローンの返済や積立貯蓄など、将来価値を求めることができますよ。
単利と複利の違い
- 単利:運用で得た利息を元本に組み入れず、最初の元本部分に対してのみ利息がでること
- 複利:運用で得た利息を元本に組み入れた運用を続けることで、利息がでること
複利は運用で得た利息を使って運用に回すことができるため、単利と複利では資産を増やすスピードが圧倒的に変わってきます。
複利の利回りについて、エクセルの関数を使ってご紹介しますね。
Table of Contents
FV関数ってなに?将来の資産価値を求める関数

エクセルのFV(フューチャー・バリュー)関数は、利率と期間から将来の投資の価値を求めることができる関数です。
FV関数を使うことで、定期支払い、定額支払い、積立貯蓄の振り込みを続けた結果、将来価値が計算できます。
投資の未来予想をエクセルで管理したい人には、楽しめる関数といえるでしょう。
今回はFV関数の基本的な使い方と、注意点について解説していきます。
FV関数の使い方は?書式と引数を解説

FV関数は投資による将来の価値を計算できる関数です。
実際にFV関数を使うために、引数について解説しますね。
FV関数の書式
FV関数の書式はこちらです。
FV関数の書式
FV(利率, 期間, 定期支払額, 現在価値, 支払期日)
FV関数の引数について解説します。
FV関数の引数
- 「利率」は必須項目で、利率を指定します。
- 「利率」は年利が3%で、毎月支払う場合は、「0.03÷12」のように指定します。
- 「期間」は必須項目で、支払回数を指定します。
- 「期間」は毎月の支払いを2年間する場合は、「2×12」のように指定します。
- 「定期支払額」は必須項目で、毎回の支払額を「マイナス」で指定します。
- 「現在価値」は最初に頭金を指定できます。省略した場合は、0が指定されたものとなります。
- 「支払期日」は支払が期首なのか、期末なのかを指定します。省略した場合は、0が指定されて期末となります。
- 「支払期日」に0以外を指定すると、期首となります。
FV関数を使うには?実例を使って解説

関数を使うための基本的な操作は、「関数の挿入」を使うことになります。
関数の挿入を使ってFV関数を使うには、タブの真下にある「fx」をクリックする必要があります。
キーボードから直接入力することも可能ですが、まずは関数の呼び出し方や使い方に慣れることを優先しましょう。
関数の挿入からFV関数を選択
関数の挿入からFV関数を使って、年利3%で5年の間、毎月5万円積み立てた結果を計算してみましょう。
FV関数を検索
- E5セルをクリック
- 「fx」をクリック
- 関数の検索をしましょう。
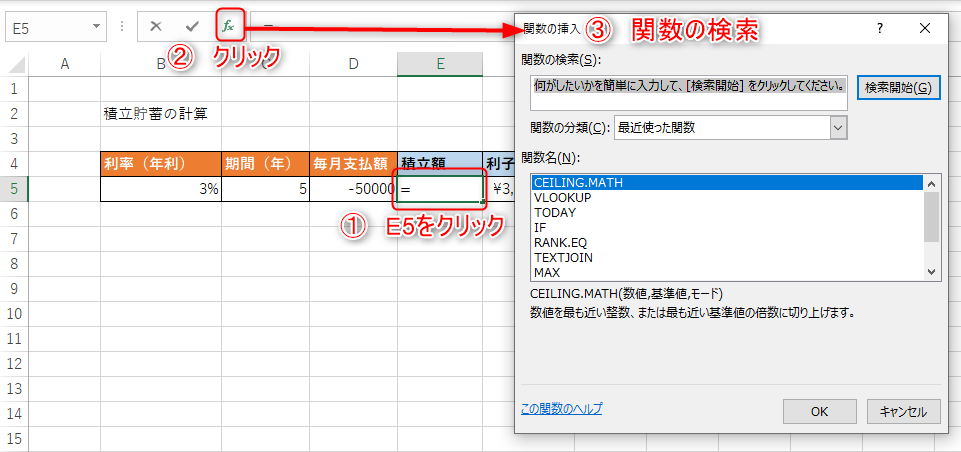
FV関数の検索方法として
FV関数の検索方法
- 「関数の検索」に「FV」を入力して検索
- 「関数の分類」に「財務」を選択
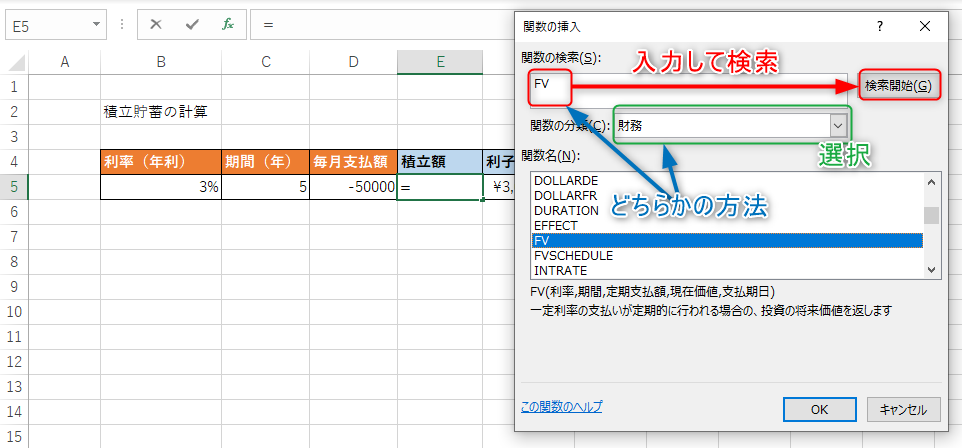
どちらかの方法を使うことで「関数名」に候補となる関数の一覧が表示されますので、「FV」を選択してOKボタンを押します。
FV関数の引数の設定
FV関数の引数の画面に移動しましたら、関数の引数には以下の値を設定しましょう。
FV関数の引数
- 「利率」に「B5/12」を入力
- 「期間」に「C5*12」を入力
- 「定期支払額」に「D5」を入力
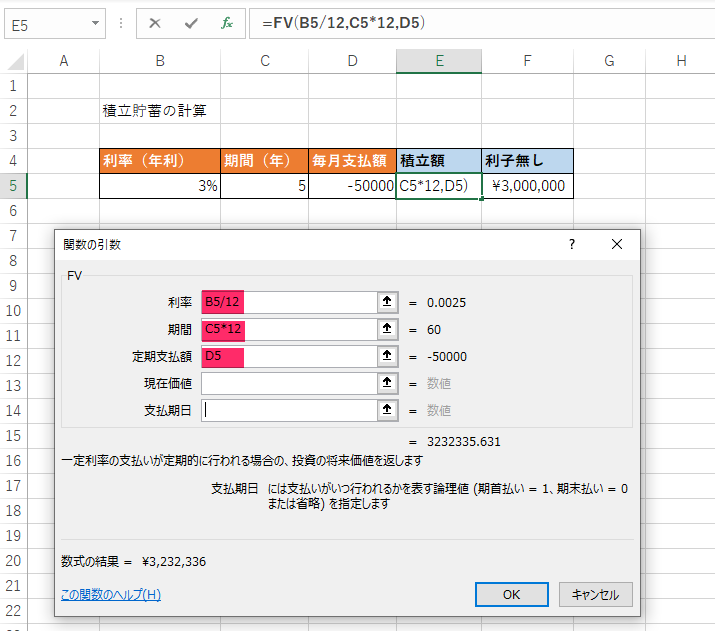
FV関数の引数は指定するときに、そのまま指定すると間違った結果が表示されてしまいます。
今回のケースでは、月払いになるように引数を合わせましょう。
引数の詳細をチェック!
- 利率は年利のため、毎月で計算するので12で割ります。
- 期間は年単位のため、毎月で計算するので12を掛けます。
- 定期支払額は手元から支払うため、マイナスとなります。
FV関数を使った結果、積立金が「¥3,232,336」となりました。

タンス預金などで利子がない場合は「¥3,000,000」になるため、差分の「¥232,336」の金額分、積み立てた方がお得だと分かりました。
期間が長ければお得なの?FV関数を使って積立額を比較

インターネットを使って手軽に投資ができるようになりました。
「投資は長期的に行うと良い」と聞いたことはありませんか?
そして、長期ってどのくらいのことなのか、FV関数を使って確認してみましょう。
FV関数の条件
- 年利:10%
- 積立期間:30年
- 毎月の支払額:5万円
- 初期投資額:100万円
- 支払期日:期末
投資の期間を5年から30年まで、FV関数を使って計算した結果を比較してみました。
また、同じ期間で利率0%のタンス預金した金額も計算していますので、どのくらいの差があるかを確認してみましょう。
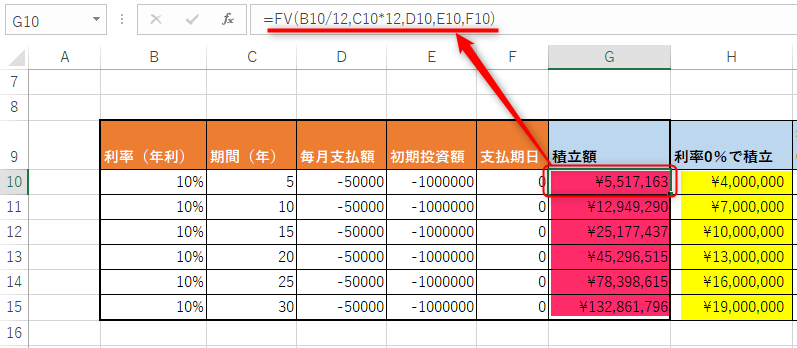
利率10%の変化は?FV関数を使って金額の成長具合を確認
100万円の初期投資をした後、毎月5万円を積立していきます。
5年ごとにどのような変化をしていくのか、年利10%と0%を比較していきましょう。
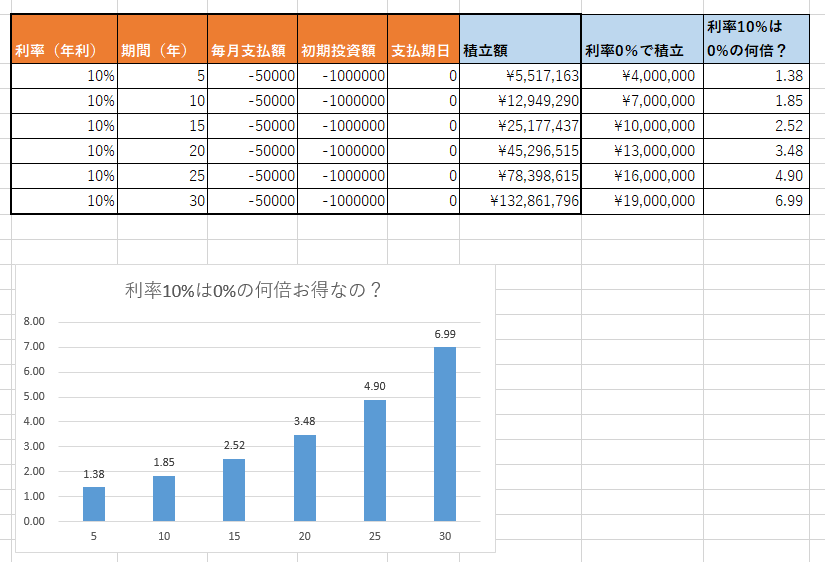
5年後の比較結果
利率10%と利率0%の積立金額を比較すると、差は1.38倍となりました。
5年後の比較結果
- 利率10%:「¥5,517,163」
- 利率0% :「¥4,000,000」
10年後の比較結果
利率10%と利率0%の積立金額を比較すると、差は1.85倍となりました。
10年後の比較結果
- 利率10%:「¥12,949,290」
- 利率0% :「¥7,000,000」
20年後の比較結果
利率10%と利率0%の積立金額を比較すると、差は3.48倍となりました。
20年後の比較結果
- 利率10%:「¥45,296,515」
- 利率0% :「¥13,000,000」
30年後の比較結果
利率10%と利率0%の積立金額を比較すると、差は6.99倍で7倍近くも積立額に差がありました。
30年後の比較結果
- 利率10%:「¥132,861,796」
- 利率0% :「¥19,000,000」
このような結果から、投資は長期的に行うことで、毎月積立している額+利益に対しても利率の計算がされるため、時間が経つほど資産の増加率が上がることがわかりますね。
このパターンとは別に、年利や期間を変更して色々試してみると、将来の資産形成に役立ちますよ。
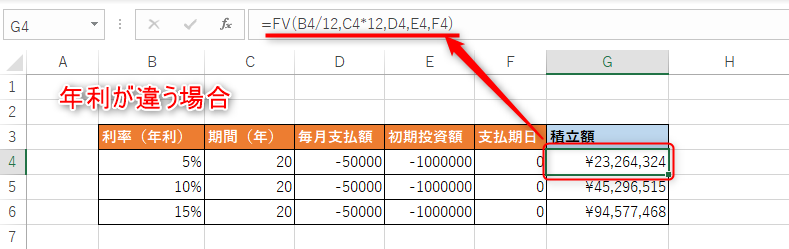
エクセルのFV関数まとめ

Excel(エクセル)のFV(フューチャー・バリュー)関数を使って、積立金の計算を確認しました。
投資などで将来の価値を求めることに使えるため、投資内容をエクセルで管理するときに活躍します。
引数の中でも「利率」「期間」「定期支払額」を指定するときには、注意が必要でしたね。
FV関数を正しく使いこなして、将来の資産を想像してみてはいかがでしょうか?楽しいと思いますよ。
